
This article will delve into what exactly put/call parity is, the exact formula for calculating it, and how becoming familiar with this concept can deepen your understanding of the options market.
What is Put/Call Parity?
Put/call parity is a concept that defines the mathematical relationship between the prices of put options and call options that have the same strike price and expiration date. In other words, if a call option is trading at X, the put option of the same strike and expiration date should be trading at Y, and vice versa.
Put simply, put/call parity realizes that you can use different combinations of options to create the same position and formalizes this mathematical relationship between puts and calls.
For instance, combining shares of the underlying with an at-the-money put is almost identical to buying an at-the-money call. Put/call parity assumes these two identical portfolios should cost the same.
To give you a visual, both our “synthetic call” position and buying a call option outright have an identical payoff, as you can see in the payoff diagram below:
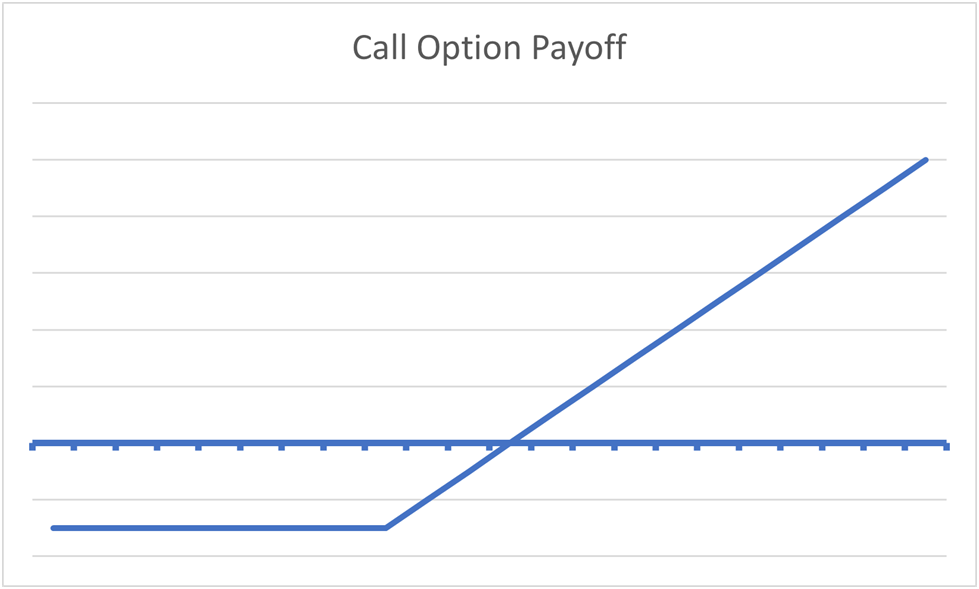
Put/call parity formalizes the mathematics behind puts and calls and gives each option a definitive intrinsic value. The introduction of synthetics means that there's a direct arbitrage component to options, ensuring that opportunistic traders always keep the prices of options in line.
For instance, a risk-free arbitrage opportunity exists if a synthetic call option could be purchased cheaper than the call option outright, incentivizing traders to push prices back to their fair values.
Put/Call Parity Formula
Put/call parity has a straightforward formula that essentially allows you to price out the fair value of a put option relative to its equivalent (same strike price and expiration date) call option and vice versa.
Put/call parity only applies to options with the same strike price and expiration date. For example, using this formula, you can compare the $101 strike put and call that both expire in 21 days, but you cannot compare the $101 strike put and $103 strike call with different expirations.
The put/call parity is as follows:
C + PV(x) = P + S
Where:
● C = the price of the call option
● P = the price of the put option
● PV (x) = the present value of the strike price
● S = current price of the underlying asset
So let's plug in some actual numbers into the formula and walk through it. We'll start with the price of the underlying.
Let’s assume the underlying is trading at $61.66, and we’re looking at the $70 strike call option, which is trading for $1.45 and expires in 25 days.
So let’s revise our formula by plugging in $1.45 for C, which is the price of the call option, and $61.66 for S, which is the price of the underlying.
$1.45 + PV(x) = P + 61.66
Now we have two values left to determine. PV(x) refers to the present value of the strike price. But what does that mean? Because an option is an agreement to buy or sell at a specified price at a date in the future, we have to discount the strike price to the present to account for the time value of money. We use the risk-free interest rate (most commonly the annualized rate of a 3-month US treasury bill) to discount the strike price to the present. At the time of writing, that rate is at 4.7%, so the math would look like this:
PV(x) = S / (1 + r)^T
Where:
● S = the strike price of the underlying
● R = the risk-free interest rate in decimals
● T = time to expiration in years, in decimals
To turn our time-to-expiration into a decimal, we simply divide our time-to-expiration by 365 as in 25/365 = 0.068
So our formula would look like this:
PV(x) = $70 / (1 / 0.047)^0.068 = $69.79
So this brings the present value of the strike price to $4076.16. So let’s plug in the last value to our formula:
$1.45 + 69.79 = P + 61.66
So to solve for P, or the price of the same-strike, same-expiration put option, we sum our call option price and the present value of our strike, which brings us to 71.24. Then we subtract the spot price of the underlying from 71.24, which is 9.58.
Being formulated in the 1960s, the put/call parity formula has some critical limitations in the modern era.
Put/Call Parity Applies to European Options
The original put/call parity formula introduced by Hans Stoll in 1969 applies specifically to European options. When introducing American-style options, the math changes a bit because you can exercise them anytime until expiration.
If you need to get more familiar with the difference, read our article on Options Settlement, which goes into the differences between European and American-style options.
But in short, European options are cash-settled and can only be exercised at expiration. American options are physically settled, which means settlement involves the actual transfer of the underlying asset, and they can be exercised at any time until expiration.
Index and futures options are European-style, while stock options are American-style options.
There is still a put/call parity relationship in American options. The math is just a bit different. See these NYU lecture notes to see a breakdown of the math.
Put/Call Parity Doesn’t Account for Dividends or Interest Payments
The next point is that the put/call parity formula doesn't consider any cash flows accrued by holding the underlying asset, like interest payments or dividends. These also alter the calculation.
If you were to plug in a bond or dividend-paying stock into the put/call parity formula, you'd find that the numbers wouldn't add up. That's because the formula doesn't account for the present value of cash flows like dividends or interest payments. You can also adapt the formula to work with cash flows, but that's beyond the scope of this article.
Put/Call Parity Doesn’t Account For Transaction Costs or Fees
And finally, the put/call parity doesn’t take any transaction costs, taxes, commissions, or any other extraneous costs into account.
Synthetic Replication
In the introduction to this article, we talked about how you can use different combinations of options to create two portfolios with identical payoffs. We mentioned how combining a put option and the underlying stock gives you the same payoff as buying a call option.
This idea is called synthetic replication. You could create a position with an identical payoff and risk profile, albeit with a different combination of securities. Getting a rough understanding of synthetics gives options traders a better grasp of the true nature of options and how they can be infinitely combined to alter your market view.
Using the building blocks of short/long puts or calls and short/long the underlying asset, you can replicate nearly any options position. Here are the basic examples:
● Synthetic Long Underlying: short put + long call
● Synthetic Short Underlying: short call + long put
● Synthetic Long call: long underlying + long put
● Synthetic Short Call: short underlying + short put
● Synthetic Long Put: short underlying + long call
● Synthetic Short Put: long underlying + short call
From here, we can discuss conversions, reversals, and box spreads, which are all arbitrage strategies traders use to exploit option prices when they deviate from put/call parity. Remember that your average trader will never make these trades, but learning how they work gives you a deeper appreciation of the options market.
Put/Call Parity: The Beginnings of Options Math
To give you a little background, back in the 1960s, the options market was very small. Even the most astute traders didn't know how to price options, and it was a wild west. Hans R. Stoll was one of the few academics to really dig into the weeds of options pricing in his seminal paper The Relationship Between Put and Call Option Prices published in 1969.
His work predated the work of Black, Scholes, and Merton’s groundbreaking Black-Scholes model in 1973.
Stoll found that sometimes these synthetic positions could be purchased for cheaper than the actual positions. For instance, if the market was very bullish on a stock and traders were buying calls, you could buy the underlying with an at-the-money and create a synthetic call option for cheaper than buying an at-the-money call option. Essentially, an arbitrage existed within the options market that wouldn't exist within an efficient market.
The Principle of No-Arbitrage
Put/call parity is a fundamental concept in options pricing, which assumes that two portfolios with identical payoffs should have the same price.
This is an extension of one of the most critical concepts in financial theory: the principle of no arbitrage. Put simply, it's the concept that you can't make risk-free profits by exploiting market inefficiencies.
To relate things directly to put/call parity, under the law of no-arbitrage, you should never be able to replicate the payoff of another portfolio and buy it for cheaper. For instance, a synthetic stock should cost the same as buying the underlying stock.
All derivative pricing models use the principle of no arbitrage as a built-in assumption, allowing the model to make estimates based on the economic reality that traders will exploit and close any pure arbitrage opportunities as they arise.
Bottom Line
Put/call parity is a fundamental concept that all intermediate options traders should become familiar with. It is usually the case that any call/put can be reconstructed using an alternative stock plus put/call (respectively) combination. Understanding put/call parity will never make a trader money, but learning these concepts is part of developing a broader awareness of how the options market works.
Related articles
- Synthetic Options Explained
- Synthetic Long Stock For Extreme Leverage
- Synthetic Short Stock – Higher Risk
- Options Equivalent Positions
- The Sell Put And Buy Call Strategy | A Synthetic Long Stock
-
The Synthetic Covered Call Options Strategy Explained
Subscribe to SteadyOptions now and experience the full power of options trading at your fingertips. Click the button below to get started!
Join SteadyOptions Now!






There are no comments to display.
Create an account or sign in to comment
You need to be a member in order to leave a comment
Create an account
Sign up for a new account. It's easy and free!
Register a new account
Sign in
Already have an account? Sign in here.
Sign In Now