
The second-order Greeks are a bit more complicated. Rather than looking at the impact on the option itself, they measure how a change in one of the same underlying parameters leads to a change in the value of a first-order Greek.
An important second-order metric is gamma. In fact, it is the only second-order Greek that option traders use with any regularity. Gamma measures the rate of change of the delta with respect to the underlying asset.
As delta is a first derivative of the price of an option, gamma is a second derivative.
To understand what all this means, we first need to take a step back and define what is the delta of an option.
Understanding Delta
Options Gamma Math
It’s not necessary to understand the math behind gamma (please feel free to go to the next section if you want), but for those interested gamma is defined more formally as the partial derivative of delta with respect to underlying stock price.
The formula is below (some knowledge of the normal distribution is required to understand it).

Delta refers to the change of a price of an option in regard to the price of the underlying security. For calls, delta ranges from 0 to 1.
For puts, it has a value of -1 and 0. Delta expresses how much the price of an option has increased or decreased when the underlying asset moves by 1 point.
Usually, when options are at the money, you can expect to see a delta of between 0.5 and -0.5. When options are far out of the money, they have a delta value close to 0, and when they are deep in the money, the delta is close to 1.
This means that, typically, call owners make a profit when the underlying stock increases in price, as this leads to a positive delta. In contrast, as puts have a negative delta value, put owners see gains when underlying stock falls.
It’s important to note that this is not always the case: when another factor is large enough, it can offset the data.
Calculating the Impact of Delta
To use the above in an example, imagine a call has a delta of 0.5. If the underlying stock increases by $1, the price of the call should rise by around $0.50.
If the underlying asset decreases by $1, the price will drop by about $0.50. This assumes, of course, that no other pricing variables change.
Now imagine that a put has a delta of -0.5. If the underlying stock increases by $1, the price of the put will drop by $0.50. If it decreases by $1, though, the price will rise by $0.50.
Option holders will notice that the delta of an option increases rapidly at a certain price range — this is called the exploding delta.
For the buyer, this is great news, as it can lead to big profits. Of course, the opposite is true for sellers on the other end of an exploding delta.
In fact, an exploding delta is a major reason why selling unhedged options incurs such a high risk.
Bear in mind, though, that whereas delta hedging can reduce directional risk from movements in price of the underlying asset, such a strategy will reduce the alpha along with the gamma. We’ll now see why that matters.
What Is Gamma?
Gamma specifies how much the delta will change when the underlying investment moves by $1 (a unit of gamma is 1/$).
In other words, whereas the delta tells you at what speed the price of the option will change, the gamma will tell you at what acceleration the change will happen.
This means that you can use gamma to predict how the delta will move if the underlying asset changes — and, therefore, how the value of the option will change.
Gamma is important because delta is only useful at a particular moment in time.
With gamma, you can figure out how much the delta of an option should change in the case of an increase or decrease in the underlying asset.
Why Do We Need Gamma?
To emphasize why gamma matters and how it adds another level of understanding to options that goes beyond delta, let’s take an example. Imagine two options have the same delta but different gamma values.
There’s no need to even use numbers in this example: it’s enough to say that one has a low gamma and the other a high gamma.
The option with the high gamma will be riskier. This is because if there is an unfavorable move in the underlying asset, the impact will be more pronounced.
In other words, if an option has a high gamma value, there is an increased likelihood of volatile swings. As most traders prefer options to be predictable, the option with the low gamma is preferable.
Another way to explain this is to say that gamma measures how stable the probability of an option is.
How Gamma Changes with the Passage of Time
As the delta of an option is dynamic, the gamma must also be constantly changing. Even minuscule movements in the underlying stock can lead to changes in the gamma.
Typically, the gamma reaches its peak value when the stock is near the strike price. As we already saw, the maximum delta value is 1.
As the delta decreases as the option moves further into or out of the money, the gamma value will move closer to 0.
Using Gamma to Measure Change in Delta
Calculating a change in the delta using gamma is quite straightforward. As an example, imagine ABC stock is trading at $47. Let’s say the delta is 0.3 and the gamma is 0.2.
In the case that the underlying stock increases in price by $1 to $48, the delta will move up to 0.5. If, instead, the stock was to decrease in price by $1 to $46, the delta would drop to 0.1.
Long and Short Options with Gamma
For holders of long options, gamma means an acceleration in profits every time the underlying asset moves $1 in their favor. They are long gamma.
This is because the gamma causes the delta of an option to increase as the option moves closer to the money or as it becomes further in the money.
Therefore, every dollar of increase in the underlying asset means a more efficient return on capital.
This same concept means that when an underlying asset moves $1 against the holder’s favor, losses decelerate.
On the flip side, the gamma poses a risk for sellers of options — since, if there’s a winner in the equation, there also has to be a loser. Just as gamma accelerates profits for holders of long options, it accelerates losses for sellers.
Similarly, as it causes losses to decelerate for the holder, it leads directional gains to decelerate for the seller.
The Importance of Correct Forecasts
No matter if you’re buying or selling, having an accurate forecast is essential. As a buyer, a high gamma that you forecast incorrectly could mean the option moves into the money and the delta moves toward 1 faster than you expect.
This will mean the delta will then become lower more quickly than you predicted.
If you’re a seller, an incorrect forecast is just as problematic. As the option you sold moves into the money, a high gamma may mean your position works against you at an accelerated rate. In the case your forecast is accurate, however, a high gamma could mean the sold option loses money faster, yielding positive results for you.
How Volatility Impacts Gamma
The gamma of options at the money is high when volatility is low. This is because low volatility occurs when the time value of an option is low. Then, you’ll see a dramatic rise when the underlying stock nears the strike price.
When volatility is high, however, the gamma is usually stable across strike prices. The reason for this is that when options are deeply in the money or out of the time, the time value tends to be substantial.
As options approach the money, there is a less dramatic time value. In turn, this leads the gamma to be both low and stable.
Expiration Risk
One more aspect to take into consideration is the expiration risk. The closer an option is to expiration, the more narrow the probability curve.
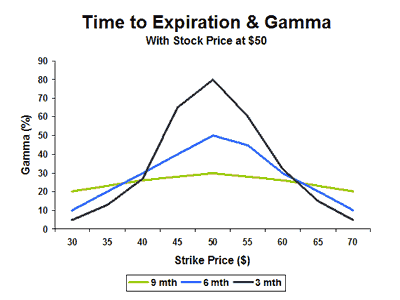
The lack of time for the underlying assets to move to far out-of-the-money strikes reduces the probability of them being in the money. The result is a more narrow delta distribution and a more aggressive gamma.
The safest way to use understanding of gamma to your advantage is to roll and close your positions at least seven (or perhaps as many as 10) days before expiration.
If you wait longer than seven days out, there’s a greater chance you’ll see drastic swings — where losing trades convert into winners and vice versa. Buyers may be able to benefit from this trend, but it is particularly risky for sellers.
List of gamma positive strategies
List of Gamma negative strategies
- Short Call
- Short Put
- Short Straddle
- Short Strangle
- Vertical Credit Spread
- Covered Call Write
- Covered Put Write
- Iron Condor
- Butterfly
- Long Calendar Spread
Summary
- Gamma measures the rate of change for delta with respect to the underlying asset's price.
- All long options have positive gamma and all short options have negative gamma.
- The gamma of a position tells us how much a $1.00 move in the underlying will change an option’s delta.
-
We never hold our trades till expiration to avoid increased gamma risk.
About the Author: Chris Young has a mathematics degree and 18 years finance experience. Chris is British by background but has worked in the US and lately in Australia. His interest in options was first aroused by the ‘Trading Options’ section of the Financial Times (of London). He decided to bring this knowledge to a wider audience and founded Epsilon Options in 2012.
Related articles
- Options Greeks: Theta, Gamma, Delta, Vega And Rho
- Options Delta Explained: Sensitivity To Price
- Options Theta Explained: Price Sensitivity To Time
- Options Vega Explained: Price Sensitivity To Volatility
- Options Rho: Sensitivity To Interest Rates
- Gamma Risk Explained
- Why You Should Not Ignore Negative Gamma
- What Is Gamma Hedging
- Market Neutral Strategies: Long Or Short Gamma?
- Estimating Gamma For Calls Or Puts
- What Is Gamma Hedging And Why Is Everyone Talking About It?
- Short Gamma Vs. Long Gamma






Create an account or sign in to comment
You need to be a member in order to leave a comment
Create an account
Sign up for a new account. It's easy and free!
Register a new account
Sign in
Already have an account? Sign in here.
Sign In Now