SteadyOptions is an options trading forum where you can find solutions from top options traders. Join Us!

We’ve all been there… researching options strategies and unable to find the answers we’re looking for. SteadyOptions has your solution.

Risk Reward Vs. Probability Of Profit

By Kim

How many times did you hear the following claims:

  • "Our system has 90% success ratio".
  • "Our trades have 1 to 4 risk reward".
  • “Always keep your reward to risk ratio greater than 1”
  • “Only take trades with a minimum of a 2:1 reward to risk ratio”
  • “If you aim for more than you risk, then you will make money.”

Lets examine those statements and see how you should put them in context and consider other parameters as well. We will use vertical spread strategy as an example.

 

Lets take a look at the following trade:

 

  • Sell to open RUT August 1175 call
  • Buy to open RUT August 1185 call

 

This is the risk profile of the trade:

 

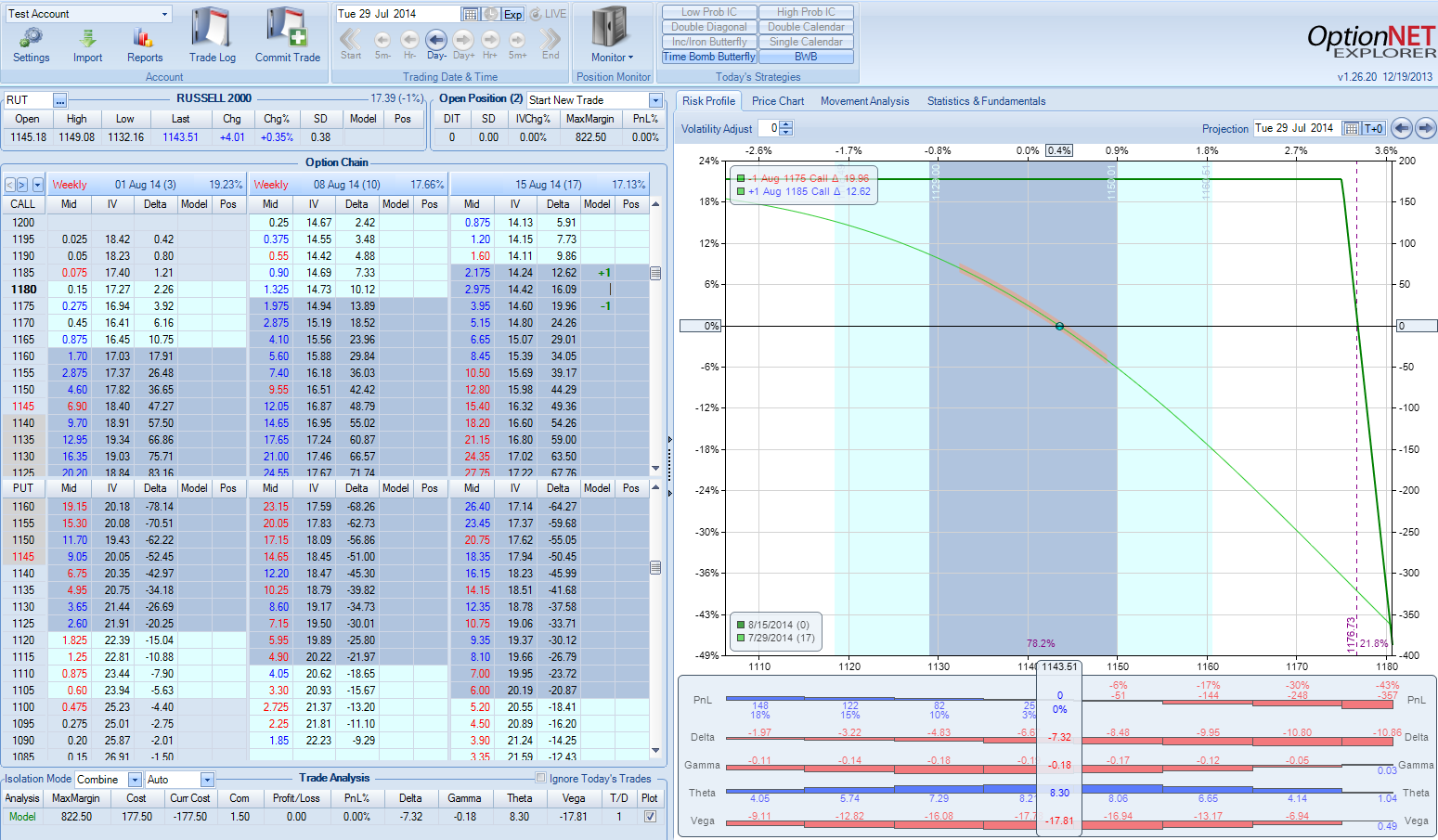
242c61bf5c2cb13bc166d07a3e4b07c9.png

 

As we can see, we are risking $822 to make $177. This is pretty bad risk reward. However, the picture looks a lot better when we look at the probability of success: it is 78%. We need the underlying to stay below 1175 by August expiration, and there is 78% chance that it will happen.

 

In this trade, bad risk/reward = high probability of success.

 

Lets take a look at another trade:

 

  • Sell to open RUT August 1100 call
  • Buy to open RUT August 1110 call

 

This is the risk profile of the trade:

 

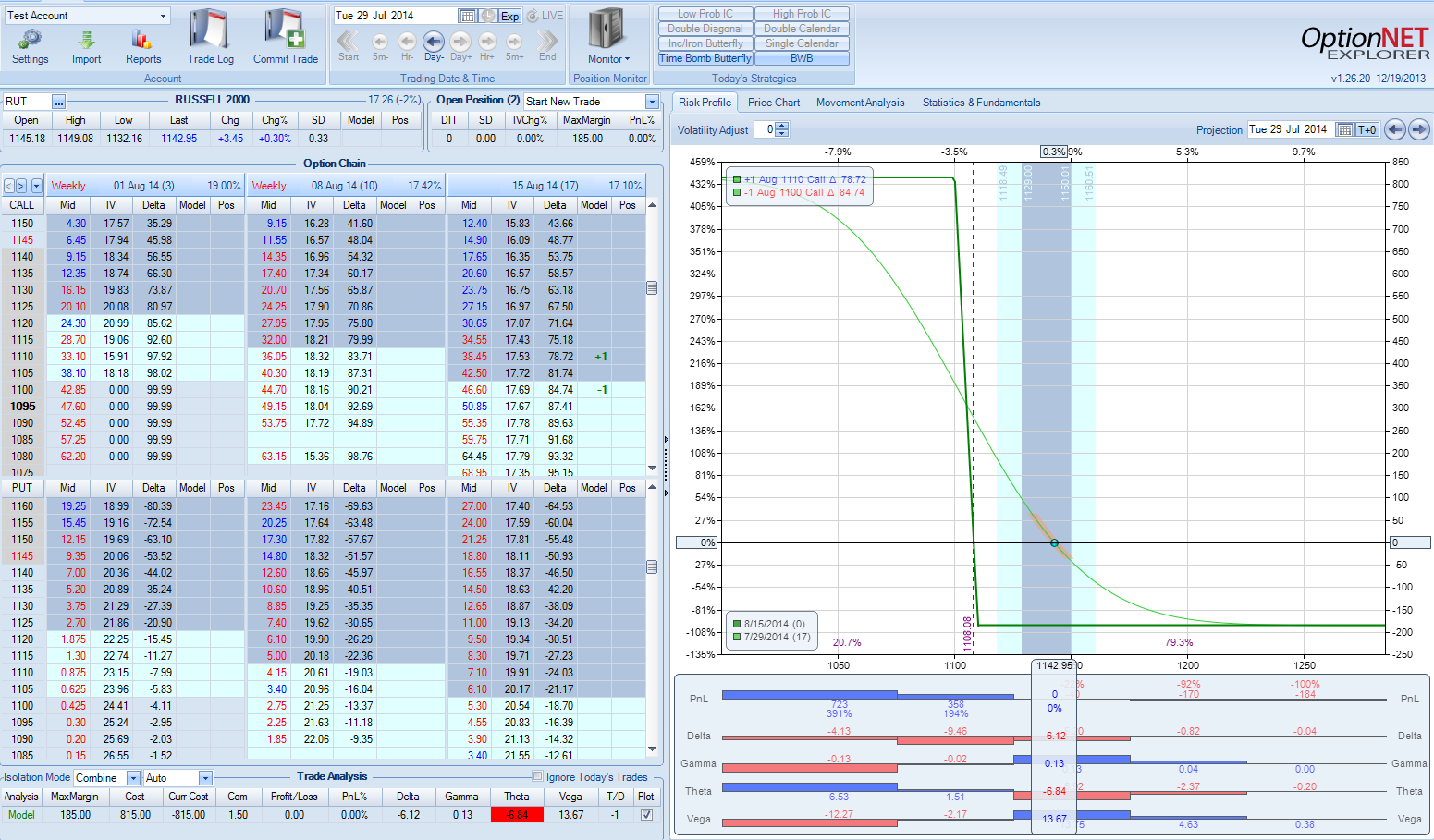
805ce5f279c5ed97f47c3bd2dc82c603.png

 

As we can see, we are risking only $185 to make $815. That's terrific risk/reward (more than 1:4). The only problem is that RUT will have to go below 1110, and there is only 20.7% probability that this will happen. (In fact, to realize the full profit, RUT has to go below 1100 and stay there by expiration).

 

In this trade, excellent risk/reward = low probability of success.

 

The following table illustrates the relation between probability of success and risk-reward:

 

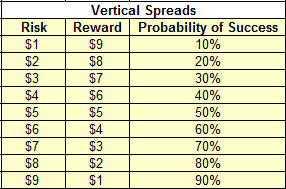
503bc5dca55716d5f4ea06ba2ea53329.png

 

Of course, this is not an exact science, but it helps us to see the approximate relation and trade-off between the risk-reward and the probability of success.

 

So next time someone will ask you: "Would you risk $9 to make $1?" - consider the context. Yes, it is a terrible risk/reward, but considering high probability of success, this is not such a bad trade. It will likely be a winner most of the time - the big question is what you do in those cases it goes against you?

 

At the same time, the answer to the question "Would you risk $1 to make $9?" is also not so obvious. It is an excellent risk/reward, but the probability to actually realize this reward is very low.

 

In trading, there is always a trade-off. You will have to choose between a good risk-reward and a high probability of success. You cannot have both.

 

Watch the video:

 


If you want to learn more about options strategies:

 

Start Your Free Trial

What Is SteadyOptions?

12 Years CAGR of 127.5%

Full Trading Plan

Complete Portfolio Approach

Real-time trade sharing: entry, exit, and adjustments

Diversified Options Strategies

Exclusive Community Forum

Steady And Consistent Gains

High Quality Education

Risk Management, Portfolio Size

Performance based on real fills

Subscribe to SteadyOptions now and experience the full power of options trading!
Subscribe

Non-directional Options Strategies

10-15 trade Ideas Per Month

Targets 5-7% Monthly Net Return

Visit our Education Center

Recent Articles

Articles

  • Harnessing Monte Carlo Simulations for Options Trading: A Strategic Approach

    In the world of options trading, one of the greatest challenges is determining future price ranges with enough accuracy to structure profitable trades. One method traders can leverage to enhance these predictions is Monte Carlo simulations, a powerful statistical tool that allows for the projection of a stock or ETF's future price distribution based on historical data.

    By Romuald,

    • 1 comment
    • 4,590 views

  • Is There Such A Thing As Risk-Management Within Crypto Trading?

    Any trader looking to build reliable long-term wealth is best off avoiding cryptocurrency. At least, this is a message that the experts have been touting since crypto entered the trading sphere and, in many ways, they aren’t wrong. The volatile nature of cryptocurrencies alone places them very much in the red danger zone of high-risk investments.

    By Kim,

    • 0 comments
    • 1,371 views

  • Is There A ‘Free Lunch’ In Options?

    In olden times, alchemists would search for the philosopher’s stone, the material that would turn other materials into gold. Option traders likewise sometimes overtly, sometimes secretly hope to find that most elusive of all option positions: the risk free trade with guaranteed positive outcome:

    By TrustyJules,

    • 1 comment
    • 17,391 views

  • What Are Covered Calls And How Do They Work?

    A covered call is an options trading strategy where an investor holds a long position in an asset (most usually an equity) and sells call options on that same asset. This strategy can generate additional income from the premium received for selling the call options.

    By Kim,

    • 0 comments
    • 2,847 views

  • SPX Options vs. SPY Options: Which Should I Trade?

    Trading options on the S&P 500 is a popular way to make money on the index. There are several ways traders use this index, but two of the most popular are to trade options on SPX or SPY. One key difference between the two is that SPX options are based on the index, while SPY options are based on an exchange-traded fund (ETF) that tracks the index.

    By Mark Wolfinger,

    • 0 comments
    • 6,894 views

  • Yes, We Are Playing Not to Lose!

    There are many trading quotes from different traders/investors, but this one is one of my favorites: “In trading/investing it's not about how much you make, but how much you don't lose" - Bernard Baruch. At SteadyOptions, this has been one of our major goals in the last 12 years.

    By Kim,

    • 0 comments
    • 4,190 views

  • The Impact of Implied Volatility (IV) on Popular Options Trades

    You’ll often read that a given option trade is either vega positive (meaning that IV rising will help it and IV falling will hurt it) or vega negative (meaning IV falling will help and IV rising will hurt).   However, in fact many popular options spreads can be either vega positive or vega negative depending where where the stock price is relative to the spread strikes.  

    By Yowster,

    • 0 comments
    • 6,540 views

  • Please Follow Me Inside The Insiders

    The greatest joy in investing in options is when you are right on direction. It’s really hard to beat any return that is based on a correct options bet on the direction of a stock, which is why we spend much of our time poring over charts, historical analysis, Elliot waves, RSI and what not.

    By TrustyJules,

    • 0 comments
    • 3,802 views

  • Trading Earnings With Ratio Spread

    A 1x2 ratio spread with call options is created by selling one lower-strike call and buying two higher-strike calls. This strategy can be established for either a net credit or for a net debit, depending on the time to expiration, the percentage distance between the strike prices and the level of volatility.

    By TrustyJules,

    • 0 comments
    • 4,921 views

  • SteadyOptions 2023 - Year In Review

    2023 marks our 12th year as a public trading service. We closed 192 winners out of 282 trades (68.1% winning ratio). Our model portfolio produced 112.2% compounded gain on the whole account based on 10% allocation per trade. We had only one losing month and one essentially breakeven in 2023. 

    By Kim,

    • 0 comments
    • 9,440 views
  • Upvote 1
  Report Article
Go to articles Trading Blog

We want to hear from you!


Guest AkramMajed

Guest AkramMajed

Posted

Trading always comes hand in hand with risk and is directly proportional to success. If don't take risk you will not succeed.

Share this comment

Link to comment
Share on other sites
Kim

Of course. But it is also important to understand the trade-off between the risk-reward and the probability of success. It is important to understand that when implementing a 90% winning ratio strategy, you sacrifice something - it doesn't come for free. 

Share this comment

Link to comment
Share on other sites
biotrader

This sounds like one of those "there isn't a right or wrong answer"... I think by place 90% probabilty trades you will be close to "picking up nickles infront of a steamroller"... on the other hand, if you do the 10% probabiliyt trades, they will be lottery tickets and you will rarely win... I don't think neither of those trades can be profitable unless you tweak that system. In the 90% chance trade, it will be that 10% that will wipe you out... 

Share this comment

Link to comment
Share on other sites
Kim

Absolutely. It all comes to trade management.

 

There is still a small edge on all those trades (10%, 90% or 50%) due to the fact that in the long term, Implied Volatility tends to be slightly higher than Historical Volatility. But the main edge comes from the trade management.

Share this comment

Link to comment
Share on other sites
CostaKapo

With the picking up nickels in front of a steamroller analogy doesn't that really only apply with the spread moves completely against you. Can't you avoid the steamroller by putting a stop loss in place? Are there brokers that have a function where you can have the strategy close out if the underlying security hits a dollar amount? You may get your arm clipped but not run over....

 

I placed an $AAPL bull put spread where I bough the Aug 15 93 put and sold the Aug 15 94 put. I collected 150$ premium and rode it out to collect 90% of the premium before closing out the trade. (The only reason I don't hold into expiration is I am trying to avoid after hours trading debacles)

 

If I had parameters in place to avoid it ever even getting to the 94 mark, wouldn't it make sense to place this trade over and over and over if the probability of success is there?

Share this comment

Link to comment
Share on other sites
Kim

Most brokers have this functionality. You just set a contingent order to close or adjust based on certain parameters. We do it all the time in our Steady Condors portfolio. 

Share this comment

Link to comment
Share on other sites
Guest uktrader

Guest uktrader

Posted

what you have forgotten to explain is that even with a 78 percent win rate you could still get 4 to 5 losing trades in a row so risking 800 to make 200 in your exanple would be a financial disaster should you run into these horrendous losing clusters

Share this comment

Link to comment
Share on other sites
Kim
1 hour ago, Guest uktrader said:

what you have forgotten to explain is that even with a 78 percent win rate you could still get 4 to 5 losing trades in a row so risking 800 to make 200 in your exanple would be a financial disaster should you run into these horrendous losing clusters

Of course. But this is true with any trade. This is where position sizing and risk management come in place. If you make 10-15% on you winning trades, you cannot afford to lose more than 20-25% on your losing trades.

There are few dimensions to every trade. Risk/reward, probability of success, risk management etc. The point is that you cannot take just one dimension (like 80% winning ratio) and say that this is what makes this trade better than others.

Share this comment

Link to comment
Share on other sites


Create an account or sign in to comment

You need to be a member in order to leave a comment

Create an account

Sign up for a new account. It's easy and free!


Register a new account

Sign in

Already have an account? Sign in here.


Sign In Now

Options Trading Blogs