Estimating Delta for Calls or Puts

Delta describes how option premium reacts to movement in the underlying security. Like a stock’s Beta, the option’s Delta is going to vary based on specific factors, notably the moneyness of the option. The farther out of the money and the longer the time to expiration, the less premium should be expected to react to underlying price changes.

A change in time value may be offset by opposite movement in extrinsic value for in-the-money contracts, and out-of-the-money options are likely to under-react to changes in the underlying. Putting this another way, the option’s volatility reacts to the underlying’s historical volatility depending on moneyness and time to expiration. This is easily overlooked in the uncertain assumptions that traders can make about volatility itself. There is nothing clear or certain about option premium behavior, and this simply is a reality that must be accepted.

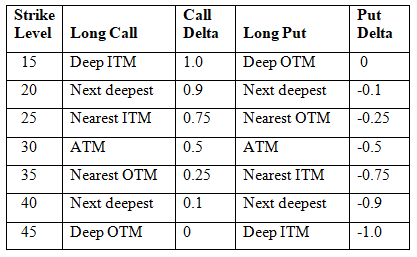
Delta – notated with the Greek letter Δ – is used to identify this often confusing relationship. It ranges between 1.0 and -01.0. The call is always a positive value from 1.0 to 0 and the put is a negative value between 0 and -1.0. An approximation of Delta can be shown in the table.

This estimate, or rule of thumb, is useful in demonstrating the workings of Delta, which naturally varies with every underlying and its character. As with all such indicators, it is most valuable when used as a comparative tool. To arrive at Delta, divide the derivation (ð) of the option (O) by the derivation (ð) f the underlying (S):
 

            Δ = ðO ÷ ðS

You may assume that Delta will move by 0.5 points for each movement in the underlying. A 2-point upward move in the underlying should create a one-point change in Delta:
 

            2 * 0.5 = 1.0

For a put, the same change is negative, so a two-point upward move creates a one-point decline:
 

            2 * -0.5 = -1.0

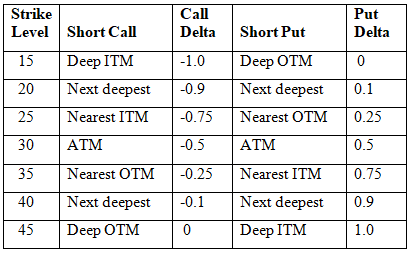
As expiration becomes closer, Delta will tend to escalate for ATM or near-ATM positions. These general “rules” for Delta are applicable for long options. They are opposite for short options, however. Duplicating the previous chart but showing Delta changes likely to be seen for short options produces the opposite outcomes:

Delta helps determine the number of open positions required to hedge a position in the underlying security. When the two sides are the same, they are at position Delta, also called a delta hedge ratio. This can also be defined in a somewhat different manner:

Delta is a measure of the dollar change in an option resulting from a dollar change in the value of the underlying asset. It is an extremely useful option-pricing statistic, being a prerequisite for the determination of an option hedge ratio. (Strong, Robert A. & Dickinson, Amy (Jan/Feb 1994). Forecasting better hedge ratios. Financial Analysts Journal, 5(1), 70)

For example, if an ATM option shows Delta of 0.5, it means there is a 50% chance it will end up ATM and a 50% chance it will move to OTM. When looked at in this manner, Delta is a moneyness probability proxy. This means you need two ATM options to hedge an underlying position. In other words, two long options will act as hedges one short position with maximum Delta of 1.0:
 

            2 * 0.5 – 1.0

This creates a “Delta neutral” situation that can be altered by changing the number of underlying positions, either long or short. For ex ample, going from two long calls to three Delta positive sets of 1.5 instead of the exact 1-to-1 hedge, sets up:

            3 * 0.5 = 1.5

This also works with puts when setting up a Delta negative, bearish position in options, involving either short calls or long puts. With the Delta range between zero and one, the relationship is shown as:

            Δ_p = Δ_c - 1      

Delta is much more than just a test comparing option premium to the underlying. It also is used to set up specific hedging strategies. The most popular is the Delta spread, where a Delta neutral position is set up like the one described above, but to hedge this, the trader also buys or sells options proportionate to the Delta neutral position. In this strategy, positive and negative Deltas are offset so that over the entire range of positions, Delta becomes zero.

A trader entering a Delta spread expects to realize a profit if the underlying security does not stray very far in its range of price. The most advantageous timing of a Delta spread is when the underlying is range-bound in a consolidation pattern. But losses are also possible, potentially large losses, if the underlying moves far above or below the middle price range.
 

This usually is set up as a calendar spread involving short-term short positions offset by longer-term long positions. Small price movements will not cause losses but will also inhibit even small profits from developing. The strategy relies on the short position losing time value and either expiring or being closed at a profit, and then hoping the long option becomes profitable or breaks even as well.
 

There is more to Delta than just comparing option to the underlying. It is most valuable when compared between two or more different underlying securities and their options, as one of many tools for picking the most favorable positions given assumptions about volatility levels.

Michael C. Thomsett is a widely published author with over 80 business and investing books, including the best-selling Getting Started in Options, coming out in its 10th edition later this year. He also wrote the recently released The Mathematics of Options. Thomsett is a frequent speaker at trade shows and blogs on his website at Thomsett Guide as well as on Seeking Alpha, LinkedIn, Twitter and Facebook.

 

Related articles

• The Options Greeks: Is It Greek To You?
• Options Trading Greeks: Theta For Time Decay
• Options Trading Greeks: Delta For Direction
• Options Trading Greeks: Gamma For Speed
• Options Trading Greeks: Vega For Volatility
• Why You Should Not Ignore Negative Gamma
• Why Delta Dollars Will Change Your Trading
• Options Greeks Explained
• Options Greeks Essentials
• Options Greeks: Myths And Realities
• Options Delta And Other Greeks
• Estimating Gamma For Calls Or Puts